http://business.sohu.com/20161221/n476529502.shtml
中金网12月21日讯,华尔街分析师周三(12月21日)撰文指出,由于多年的业绩糟糕但却收费高昂,客户们正在纷纷赎回在对冲基金的投资。
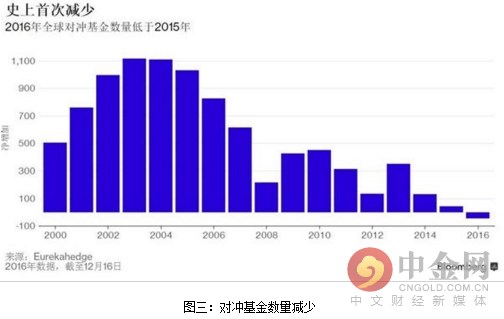
分析师称:“行业内对冲基金的数量有史以来第一次出现减少,而很多全球闻名遐迩的对冲基金公司也被迫降低费率。不过,这个行业在上个月却得到一个意想不到的帮助,随着特朗普当选美国总统引发的市场波动提高了对冲基金的回报,不仅扭转了一些基金的运程,也预示未来会有好日子。”
分析师还指出,规模3万亿美元的全球对冲基金行业在客户们此起彼伏的抱怨中走向2017年。要知道,亚洲对冲基金自2011年以来首次表现落后于全球同业,有可能在乏善可陈的表现和高收费遭到全球抵制之际进一步削弱投资者信心。根据Eurekahedge的数据,今年1-11月,他们仅实现了0.8%的增长,全年回报率或将降至五年来最低水平。
根据数据供应商eVestment的初步估算,今年截至12月16日,投资者从对冲基金撤资近800亿美元,为2009年以来该行业首次遭遇净赎回。业内一些大牌公司,例如Brevan Howard Asset Management、奥奇-齐夫资本管理集团和John Paulson麾下的对冲基金都遭遇资金流出。
这个行业传统的2%管理费加20%业绩分成的收费模式有点行不通了。Louis Bacon的Moore Capital Management、Tudor Investment Corp。、奥奇-齐夫资本管理集团、Canyon Capital Advisors和Brevan Howard Asset Management等公司今年都降低了收费。
全球对冲基金的数量在今年出现下降,是Eurekahedge自2000年开始汇总这一数据以来首次出现这种情况。欧洲对冲基金数量减少最多,那里糟糕的业绩表现、不断增加的监管合规成本和投资者的不待见导致关闭的对冲基金数量超过新设数量。
全球对冲基金管理的总资产连续8年增加,截至9月底达到2.97万亿美元,主要是因为投资回报带来资产增加抵消了投资者的赎回。
对冲基金的基金行业有望遭遇3年来最高年度资金净流出,因为客户继续选择弃用中介,转而直接投资。对冲基金研究公司(Hedge Fund Research Inc.)的数据显示,截至9月底,全球经营中的对冲基金的基金数量已经从2007年的2,462个降至1,577个。这些基金管理的资产规模同期减少1,620亿美元,降至6,363亿美元。
在养老基金、捐赠基金和保险公司等大型投资者的引领下,投资越来越集中于少数知名对冲基金公司。对冲基金研究公司的数据显示,资产规模50亿美元以上的对冲基金总计管理全行业68.6%的资产,高于2009年底的61%。2008年金融危机之后,投资者钟爱大型对冲基金公司的安全性,令这一趋势进一步加速。
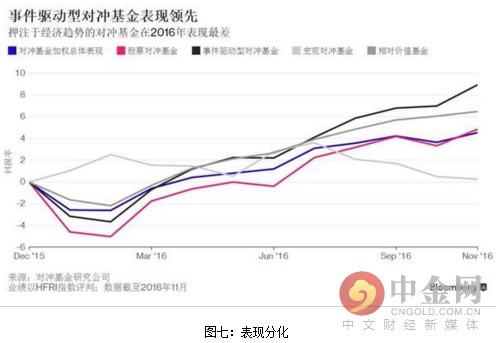
今年截至11月份,对冲基金回报率4.5%,主要得益于下半年的表现和唐纳德·特朗普意外当选之后引发的市场波动性。根据对冲基金研究公司的数据,以企业事件为主题的对冲基金表现最好,押注于宏观经济趋势的对冲基金则不尽如意。
在大数据时代,越来越多的对冲基金选择通过量化策略来赚钱,投资者也向此类基金投入更多资本。根据eVestment的数据,利用数学模型进行跨资产押注的对冲基金策略管理期货(Managed futures)截至10月份吸引193亿美元资金流入,而业内其他策略则是资金净流出。
英国依然是欧洲的对冲基金中心,2016年,全球20%的对冲基金集中于此,比例高于2010年的18%。不过,英国公投决定脱离欧盟,已经引起了一些基金公司和投资者的担忧。数据供应商Preqin的一项调查发现,6%的对冲基金正在考虑搬出英国,而7月份仅有3%的基金有此考虑。
在1月份大跌8.8%之后,以大中华为对象的对冲基金今年截至11月份平均亏损2.5%。Eurekahedge跟踪的基金中,大约97%大中华对冲基金在1月份都亏损,高于全亚洲83%的比例。截至11月份,68%的大中华对冲基金依然亏损,但全亚洲亏损基金比例已经降至45%。今年截至11月份,恒生中国企业指数上涨了1.8%。